
Welcome to SALSA’s documentation!¶
SALSA: Software Lab for Advanced Machine Learning with Stochastic Algorithms is a native Julia implementation of stochastic algorithms for:
- linear and non-linear Support Vector Machines
- sparse linear modelling
SALSA is an open source project available at Github under the GPLv3 license.
Installation¶
The SALSA package can be installed from the Julia command line with Pkg.add("SALSA") or by running the same command directly with Julia executable by julia -e 'Pkg.add("SALSA")'.
Mathematical background¶
The SALSA package aims at stochastically learning a classifier or regressor via the Regularized Empirical Risk Minimization [Vapnik1992] framework. We approach a family of the well-known Machine Learning problems of the type:
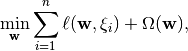
where 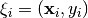 is given as a pair of input-output variables and belongs to a set
is given as a pair of input-output variables and belongs to a set 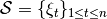 of independent observations, the loss functions
of independent observations, the loss functions 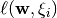 measures the disagreement between the true target
measures the disagreement between the true target 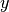 and the model prediction
and the model prediction 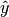 while the regularization term
while the regularization term 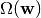 penalizes the complexity of the model
penalizes the complexity of the model 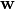 . We draw uniformly
. We draw uniformly 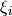 from
from 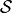 at most
at most 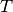 times due of the i.i.d. assumption and a fixed computational budget. Online passes and optimization with the full dataset are available too. The package includes stochastic algorithms for linear and non-linear Support Vector Machines [Boser1992] and sparse linear modelling [Hastie2015].
times due of the i.i.d. assumption and a fixed computational budget. Online passes and optimization with the full dataset are available too. The package includes stochastic algorithms for linear and non-linear Support Vector Machines [Boser1992] and sparse linear modelling [Hastie2015].
Particular choices of loss functions are (but are not restricted to the selection below):
Particular choices of the regularization term are:
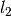 -regularization, i.e.
-regularization, i.e. 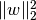
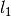 -regularization, i.e.
-regularization, i.e. 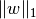
- reweighted
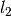 -regularization
-regularization - reweighted
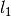 -regularization
-regularization
References¶
SALSA is stemmed from the following algorithmic approaches:
- Pegasos: S. Shalev-Shwartz, Y. Singer, N. Srebro, Pegasos: Primal Estimated sub-GrAdient SOlver for SVM, in: Proceedings of the 24th international conference on Machine learning, ICML ’07, New York, NY, USA, 2007, pp. 807–814.
- RDA: L. Xiao, Dual averaging methods for regularized stochastic learning and online optimization, J. Mach. Learn. Res. 11 (2010), pp. 2543–2596.
- Adaptive RDA: J. Duchi, E. Hazan, Y. Singer, Adaptive subgradient methods for online learning and stochastic optimization, J. Mach. Learn. Res. 12 (2011), pp. 2121–2159.
- Reweighted RDA: V. Jumutc, J.A.K. Suykens, Reweighted stochastic learning, Neurocomputing Special Issue - ISNN2014, 2015. (In Press)
Dependencies¶
- MLBase: to support generic Machine Learning routines
- StatsBase: to support generic routines from Statistics
- Distances: to support distance metrics between vectors
- Distributions: to support sampling from various distributions
- DataFrames: to support and process files instead of in-memory matrices
- Clustering: to support Stochastic K-means Clustering (experimental feature)
- ProgressMeter: to support progress bars and ETA of different routines
Indices and tables¶
| [Vapnik1992] | Vapnik, Vladimir. “Principles of risk minimization for learning theory”, In Advances in neural information processing systems (NIPS), pp. 831-838. 1992. |
| [Boser1992] | Boser, B., Guyon, I., Vapnik, V. “A training algorithm for optimal margin classifiers”, In Proceedings of the fifth annual workshop on Computational learning theory - COLT‘92., pp. 144-152, 1992. |
| [Hastie2015] | Hastie T., Tibshirani R., Wainwright M. Statistical Learning with Sparsity: The Lasso and Generalizations, Chapman & Hall/CRC Monographs on Statistics & Applied Probability, 2015. |